(By Ludmila Carone)
A transit? What is that?
Here is a link to Venus as it transits in front of our Sun in 2012.
Extrasolar planets do something similar in front of their own central star. Only we cannot see it as directly as we can see it with Venus. Indirectly, however, we can if we keep the brightness of the star firmly in view:
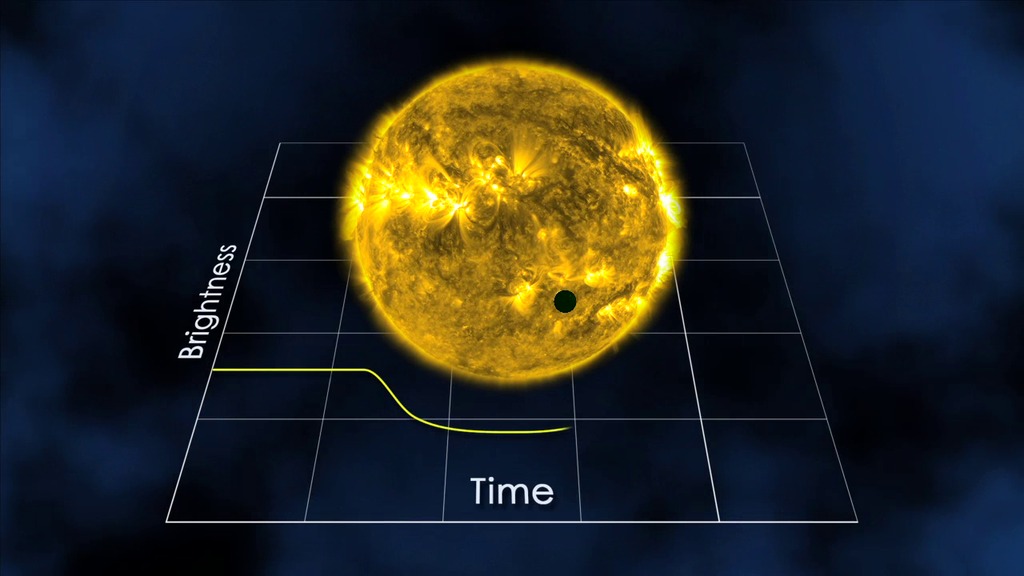
Credit: NASA/JPL-Caltech
But of course, this only works if the orbit of the planet is aligned ‘just so’ that it goes in front of its own Sun as seen from the Earth. So we need luck to track down a planet this way. This luck – i.e. the probability – of seeing a planetary transit can actually be calculated.
Luck is when skill and opportunity come together
We first assume that there is no reason why planets should prefer a certain plane in their motion around their central star. The inclination of the orbital plane can therefore, seen from us, assume all possible angles. But what must the inclination look like for us to be able to see a planetary transit at all?
The following picture shall clarify it:
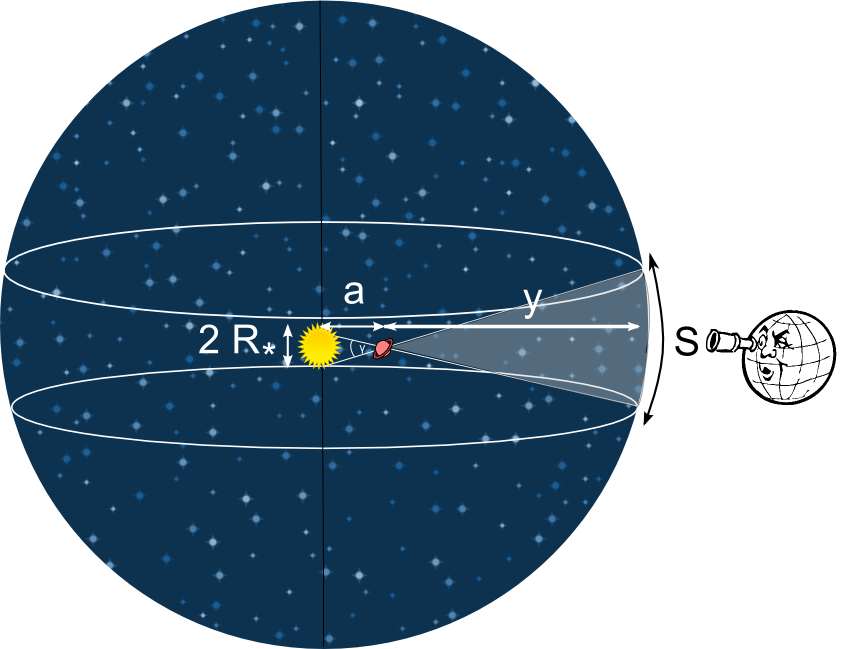
Credit: L. Carone, MPIA.
We are located at about distance y from a star. A planet orbits around this star in the horizontal plane at distance a. However, we only see the planet passing in front of its star if the inclination of the orbital plane is within the angle gamma, that is, within the grey shaded area. If we would turn the orbital plane by 90 degrees, than the planet would be outside of the grey area and thus also outside our field of view.
This also works the other way around, extraterrestrial astronomers could be able to see the transit of the planets in the Solar System if they are located within a certain angle. Very recently, Lisa Kaltenegger and Joshua Pepper calculated that Earth could be seen to transit from about 1000 stars.
Should we actually manage to establish radio contact with an extraterrestrial civilisation, it would certainly be interesting to compare the lists of detected extrasolar planets at some point. Amongst various other things, 
The ratio between the total surface of the sphere (all possible points of view at distance y) and the small segment within the two white circles (the possible points of view at distance y for which a transit becomes visible) is then:![]()
Where S is:
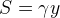
We also now assume that y is much, much larger than a and that therefore a+y is almost the same as y and replace the remaining gamma with this relation
![]() ,
,
we get a fairly simple equation to determine to first order the transit probability of a given planetary system:
![]() .
.
The tip of an iceberg. But what an iceberg!
So far, the transit method has been immensely successful. Kepler, the NASA exoplanet transit detection satellite, alone discovered over 2600 exoplanets. Not only that! Kepler’s planet census found out that the two most common type of planets out there are Super-Earths and Mini-Neptunes, objects for which there are no counterparts in the Solar System known. Thus, Kepler even though it fished with a very limited “net” (the transit method) showed us that at least 50-30% of all sun-like stars in the Milky Way have at least one planet. Kepler also showed us that there are very weird planets out there, which we did not expect – at all.
